Kuhn Mapping for Kremer-Grest polymer models V0.9

NOTICE: The current version is a development version. Please wait for V1.0 before using any of these values!!

The Kremer-Grest (KG) model is the defacto standard for coarse-grain modeling of polymers using Molecular Dynamics. It represents a polymer as a string of beads. The beads are essentially hard spheres and the springs increase in stiffness to prevent chains from passing through each other. So far there is somewhat more than 1500 papers studying various aspects of polymer physics using the KG model. The KG model is a generic model, and was not designed to match any particular specific polymer chemistry.

Below is a tool for 1) mapping real polymers to a Kuhn representation, and 2) deriving a Kremer-Grest model matching a given Kuhn representation, that we have developed based on our recent papers on Kuhn mapped KG models. Combining the two, we can derive a KG model matching the large scale emergent properties of any commodity polymer species.

The mapping

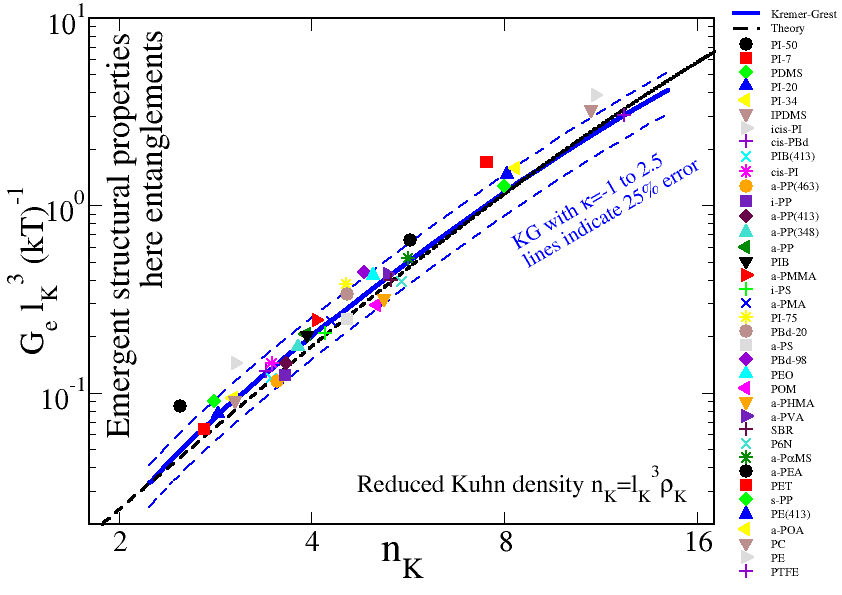
Our mapping is based on Univerality rather than explicit coarse-graining. Universality suggests that all physical properties (for concentrated polymer solutions/melts above the glass-transition temperature) depends on just two numbers. The Kuhn number which determines the chemistry of the polymers, we want to describe, and the number of Kuhn segments per chain describes the chain length of the polymer melt we are targetting. The plot above shows how by varying a single parameter - the chain stiffness - we can design KG polymer models that match fairly accurately the entanglement modulus of most commodity polymers (symbols). The entanglement modulus is just one univeral emergent quantity, we expect all other universal emergent quantities to be equally well matched.

Note that if you are interested in studying e.g. glassy dynamics or other non-universal properties which depends critically on the specific monomeric structure and interactions, then the current approach will most probably fail. You might use well equilibrated KG polymer models as a stepping stone to specific coarse-grained models or models based on atomistic force fields.

Citations for mapping.

Please cite the papers and site, if you use the mapping tool:

"Kremer Grest Models for Commodity Polymer Melts: Linking Theory, Experiment, and Simulation at the Kuhn Scale.” R. Everaers, H. A. Karimi-Varzaneh, F. Fleck, N. Hojdis, C. Svaneborg. Macromolecules 53, 1901 (2020)
"Characteristic Time and Length Scales in Melts of Kremer-Grest Bead Spring Polymers with Wormlike Bending Stiffness” C. Svaneborg, R. Everaers. Macromolecules 53, 1917 (2020)
"Kuhn Mapping for Kremer-Grest polymer models V X.Y" C. Svaneborg 2020. http://polymer.zqex.dk

Mapping tool

Below is our online tool for mapping real polymers to a Kuhn description, and mapping a Kuhn description to a KG model. If you already have a Kuhn mapping you can jump to "Kuhn mapped KG model" and enter the numbers to generate a corresponding KG model. If not, then start by entering the single chain properties. Clicking Calculate will derive quantities that you need to propagate the properties.

Single chain properties

Please enters the single-chain properties below or choose a polymer from the Polymer Handbook Polymer:

Mean square extension per unit mass <R^2>/M = (Å^2/[g/mol])
Contour-length per monomer= (Å)
Maximal extension/chain contour length Rmax/L=alpha= (0.83 for PE chains due to 68degree bond angles)
Molecular mass of monomer Mm= (g/mol)
Number of monomers per chain Nm= (number)

The maximal length is the length if you pull the chain to a straight line, but retaining the molecular structure due to valence angles. For say a PE chain, Rmax=L cos(theta/2) = 0.83*L, L total contour length of back-bone bonds, and theta=68 degrees the valence angle of a C-C-C bond.

Physical properties

The following can be predicted using the single-chain properties above, otherwise please enter:
Mean-square end-to-end extension <R^2>= (Å^2)
Maximal length Rmax= (Å)
Molecular weight of polymer chain Mc= (g/mol)
Number of monomers per chain Nm= (number)

Additional parameters are needed for the Kuhn description:

Temperature T= (K)
Bulk density rho= (g/cm^3)
Entanglement modulus Ge= = 5GN/4 (MPa)

Kuhn description of polymer

Kuhn Number nK=
Kuhn length lK= (Å)
Kuhn mass mK= (g/mol)
Monomers per Kuhn unit
Kuhn density rho_K= number/Å^3
Number of Kuhn segments in polymer Nk=
Number of Kuhn segments per entanglement NeK=
Tube diameter dT= (Å)
Packing length p= (Å)
alpha=app/p=
Temperature T= (K)

Kuhn mapped KG model

The following numbers are required for deriving a Kuhn mapped KG model:
Name of polymer:
Kuhn Number nK= (number)
Kuhn length lK= (Å)
Kuhn mass MK= (g/mol)
Kuhn segments per chain NK= (number)

KG force field

Stiffness kappa= (number)
Kuhn length lk= (sigma)
beads per Kuhn segment cb= (number)
Number of beads per chain Nb=
Number of entanglements per chain Z=
Number of Kuhn segments per entanglement: NeK=
Kuhn time: tauk=(tau)
Entanglement time: taue=(tau)
Rouse time: taur=(tau)
Maximal relaxation time: taumax=(tau)
To generate a time mapping, additional experimental input is required on one of the time scales above.

Mapping from KG units to SI units

KG bead mass mb= (g/mol)
KG length scale sigma= (Å)
KG energy unit epsilon= (J)
KG unit of stress: 1epsilon/sigma^3= (MPa)

LAMMPS script

If you have derived the KG force field above, then to generate a LAMMPS script for running the force field

References:

"Molecular dynamics simulation for polymers in the presence of a heat bath" Gary S. Grest and Kurt Kremer. Phys. Rev. A 33, 3628 (1986)
"Chain Dimensions and Entanglement Spacings." Fetters L.J., Lohse D.J., Colby R.H. (2007) In: Mark J.E. (eds) Physical Properties of Polymers Handbook. Springer, New York, NY

Contact:

In case of questions, bugs, etc. please contact Carsten Svaneborg at zqex(at)sdu(dot)dk